Quadratic Probing And Linear Probing : Java Program Source Code
Quadratic Probing and Linear Probing are the techniques to avoid collision in the hash tables . Suppose the hash value generated is already occupied in the hash table , then quadratic probing or linear probing helps to find a lace in the hash table
Quadratic Probing takes arbitrary quadratic polynomial and add it to the original hash index . The arbitrary quadratic polynomial is added till the hash value generated is not occupied in the hash table .
It works on the following formula
For a original hash index H , H+1*1 , H+2*2 ,H+3*3 ,H+4*4......
Read Also : Hamming Distance : Nucleic Acid Bases String
Linear Probing is somewhat easy , it search sequentially in the hash table for a given hash value . It does not involve any arbitrary polynomial value .
Linear probing including two values one is starting value and other is interval value . If the hash value is occupied at starting point then the next hash value is calculated by adding the interval value to the starting value . If , it is also occupied in the hash table , then again we add interval value to the hash value generated .
Then again we keep looking for the hash value for which the hash table has no entry .
It works on the following formula
For a starting value H and interval value 1 : H, H+1,H+2 , H+3,H+4.....
Pseudo code is given below :
Quadratic Probing algorithm to insert key in the hash table
1. Retrieve key k
2. Compute hash function h[k] = k % size of the table
3. If hash table is empty at the computed hash value place
then insert key at h[k]
else
we need to find another empty place in the hash table to insert the key in the hash table
3.1 Use quadratic probing to compute the hash value of the key again
3.2 If hash table place is empty then insert key at h[k] and exit
else
Repeat 3.1 step again
Read Also : Snakes And Ladder Game
Linear Probing algorithm to insert key in the hash table
1. Retrieve key k
2. Compute hash function h[k]= k %size of the table
3. If hash table is empty at the computed hash value place
then insert key at h[k]
else
we need to find another empty place in the hash table to insert the key in the table
3.1 Use linear probing to compute the hash value of the key again , in linear probing we generally
keep adding some constant value to the computed hash value .
3.2 If hash table place is empty then insert key at h[k] and exit
else
Repeat 3.1 step again .
Read Also : Langton's Ant : Java Program Code Explain
Demo :
Code :
Quadratic Probing takes arbitrary quadratic polynomial and add it to the original hash index . The arbitrary quadratic polynomial is added till the hash value generated is not occupied in the hash table .
It works on the following formula
For a original hash index H , H+1*1 , H+2*2 ,H+3*3 ,H+4*4......
Read Also : Hamming Distance : Nucleic Acid Bases String
Linear Probing is somewhat easy , it search sequentially in the hash table for a given hash value . It does not involve any arbitrary polynomial value .
Linear probing including two values one is starting value and other is interval value . If the hash value is occupied at starting point then the next hash value is calculated by adding the interval value to the starting value . If , it is also occupied in the hash table , then again we add interval value to the hash value generated .
Then again we keep looking for the hash value for which the hash table has no entry .
It works on the following formula
For a starting value H and interval value 1 : H, H+1,H+2 , H+3,H+4.....
Pseudo code is given below :
Quadratic Probing algorithm to insert key in the hash table
1. Retrieve key k
2. Compute hash function h[k] = k % size of the table
3. If hash table is empty at the computed hash value place
then insert key at h[k]
else
we need to find another empty place in the hash table to insert the key in the hash table
3.1 Use quadratic probing to compute the hash value of the key again
3.2 If hash table place is empty then insert key at h[k] and exit
else
Repeat 3.1 step again
Read Also : Snakes And Ladder Game
Linear Probing algorithm to insert key in the hash table
1. Retrieve key k
2. Compute hash function h[k]= k %size of the table
3. If hash table is empty at the computed hash value place
then insert key at h[k]
else
we need to find another empty place in the hash table to insert the key in the table
3.1 Use linear probing to compute the hash value of the key again , in linear probing we generally
keep adding some constant value to the computed hash value .
3.2 If hash table place is empty then insert key at h[k] and exit
else
Repeat 3.1 step again .
Read Also : Langton's Ant : Java Program Code Explain
Demo :
Code :
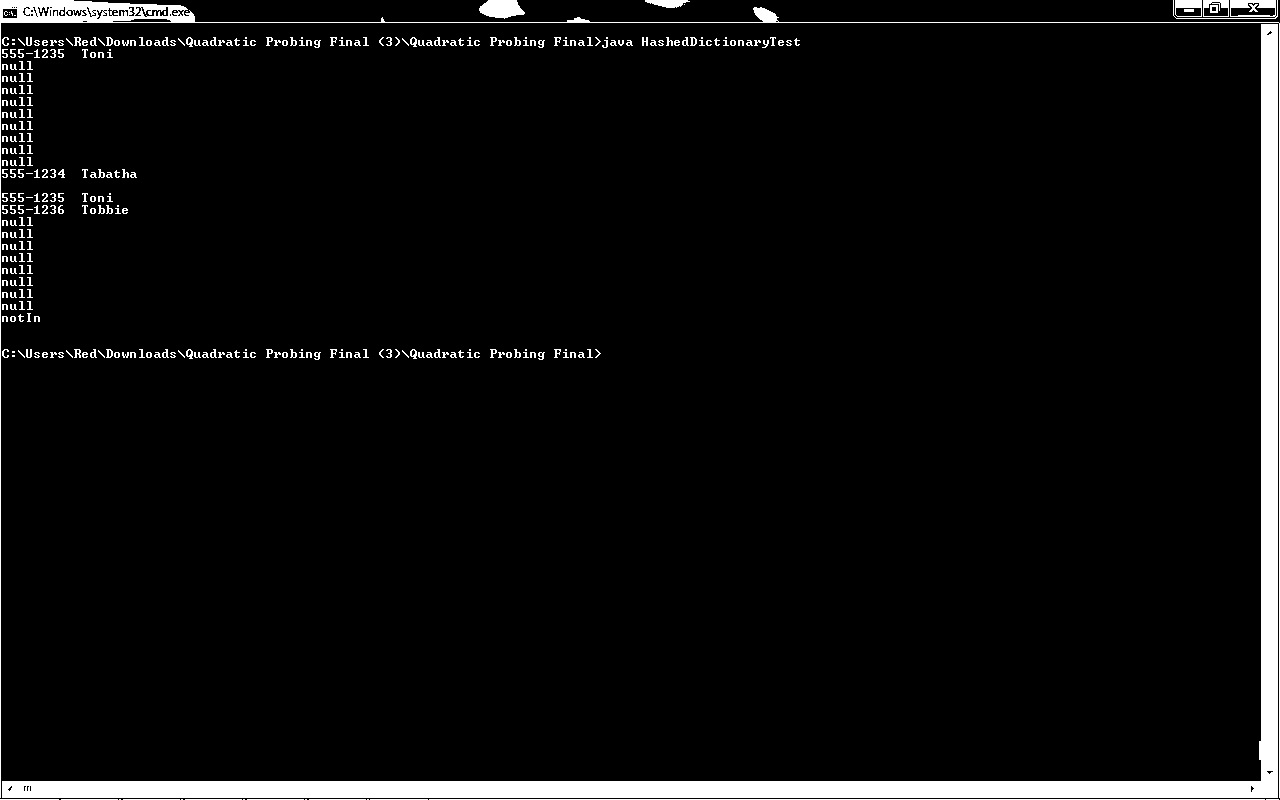
/** * A class that implements the ADT dictionary by using hashing * and linear probing to resolve collisions. * The dictionary is not sorted and has distinct search keys. * Notes: Uses probe for add, but locate for remove and getValue. * Uses linear probing, but includes code for quadratic probing. * Has a display method for illustration and testing. * * @author Sonia * @version 2.0 */ public class HashedDictionary<K, V> { public TableEntry<K, V>[] hashTable; // dictionary entries private int numberOfEntries; private int locationsUsed; // number of table locations not null private static final int DEFAULT_SIZE = 101; // must be prime private static final double MAX_LOAD_FACTOR = 0.5; // fraction of hash table that can be filled public HashedDictionary() { this(DEFAULT_SIZE); // call next constructor } // end default constructor public HashedDictionary(int tableSize) { // ensure that table is prime size at least as big as user wants; // if tableSize is prime, do not change it int primeSize = getNextPrime(tableSize); hashTable = new TableEntry[primeSize]; numberOfEntries = 0; locationsUsed = 0; } // end constructor // ------------------------- // We've added this method to display the hash table for illustration and testing // ------------------------- public void display() { for (int index = 0; index < hashTable.length; index++) { if (hashTable[index] == null) System.out.println("null "); else if (hashTable[index].isRemoved()) System.out.println("notIn "); else System.out.println(hashTable[index].getKey() + " " + hashTable[index].getValue()); } // end for System.out.println(); } // end display // ------------------------- // 20.14 public V add(K key, V value) { V oldValue; if (isHashTableTooFull()) rehash(); int index = getHashIndex(key); index = quadraticProbe(index, key); assert (index >= 0) && (index < hashTable.length); if ( (hashTable[index] == null) || hashTable[index].isRemoved()) { // key not found, so insert new entry hashTable[index] = new TableEntry<K, V>(key, value); numberOfEntries++; locationsUsed++; oldValue = null; } else { // key found; get old value for return and then replace it oldValue = hashTable[index].getValue(); hashTable[index].setValue(value); } // end if return oldValue; } // end add // 20.12 public V remove(K key) { V removedValue = null; int index = getHashIndex(key); index = locate(index, key); if (index != -1) { // key found; flag entry as removed and return its value removedValue = hashTable[index].getValue(); hashTable[index].setToRemoved(); numberOfEntries--; } // end if // else not found; result is null return removedValue; } // end remove // 20.11 public V getValue(K key) { V result = null; int index = getHashIndex(key); index = locate(index, key); if (index != -1) result = hashTable[index].getValue(); // key found; get value // else not found; result is null return result; } // end getValue // 20.15 private int quadraticProbe(int index, K key) { boolean found = false; int removedStateIndex = -1; // index of first location in // removed state int i=0; while ( !found && (hashTable[index] != null) && i< hashTable.length) { if (hashTable[index].isIn()) { if (key.equals(hashTable[index].getKey())) found = true; // key found else // follow probe sequence { index = (index + i*i) % hashTable.length; // linear probing i++; } } else // skip entries that were removed { // save index of first location in removed state if (removedStateIndex == -1) removedStateIndex = index; index = (index + i*i) % hashTable.length; // linear probing i++ ; } // end if } // end while // Assertion: either key or null is found at hashTable[index] if (found || (removedStateIndex == -1) ) return index; // index of either key or null else return removedStateIndex; // index of an available location } // end probe // 20.13 public int locate(int index, K key) { boolean found = false; int i=0; while ( !found && (hashTable[index] != null) && i<hashTable.length) { if ( hashTable[index].isIn() && key.equals(hashTable[index].getKey()) ) found = true; // key found else // follow probe sequence { index = (index + i*i) % hashTable.length; // linear probing i++; } } // end while // Assertion: either key or null is found at hashTable[index] int result = -1; if (found) result = index; return result; } // end locate public boolean contains(K key) { return getValue(key) != null; } // end contains public boolean isEmpty() { return numberOfEntries == 0; } // end isEmpty public boolean isFull() { return false; } // end isFull public int getSize() { return numberOfEntries; } // end getSize public final void clear() { for (int index = 0; index < hashTable.length; index++) hashTable[index] = null; numberOfEntries = 0; locationsUsed = 0; } // end clear public int getHashIndex(K key) { int hashIndex = key.hashCode() % hashTable.length; if (hashIndex < 0) { hashIndex = hashIndex + hashTable.length; } // end if return hashIndex; } // end getHashIndex /** Task: Increases the size of the hash table to a prime > twice its old size. */ private void rehash() { TableEntry<K, V>[] oldTable = hashTable; int oldSize = hashTable.length; int newSize = getNextPrime(oldSize + oldSize); hashTable = new TableEntry[newSize]; // increase size of array numberOfEntries = 0; // reset number of dictionary entries, since // it will be incremented by add during rehash locationsUsed = 0; // rehash dictionary entries from old array to the new and bigger // array; skip both null locations and removed entries for (int index = 0; index < oldSize; index++) { if ( (oldTable[index] != null) && oldTable[index].isIn() ) add(oldTable[index].getKey(), oldTable[index].getValue()); } // end for } // end rehash /** @return true if lambda > MAX_LOAD_FACTOR for hash table; * otherwise returns false. */ private boolean isHashTableTooFull() { return locationsUsed > MAX_LOAD_FACTOR * hashTable.length; } // end isHashTableTooFull private int getNextPrime(int integer) { // if even, add 1 to make odd if (integer % 2 == 0) { integer++; } // end if // test odd integers while(!isPrime(integer)) { integer = integer + 2; } // end while return integer; } // end getNextPrime private boolean isPrime(int integer) { boolean result; boolean done = false; // 1 and even numbers are not prime if ( (integer == 1) || (integer % 2 == 0) ) { result = false; } // 2 and 3 are prime else if ( (integer == 2) || (integer == 3) ) { result = true; } else // integer is odd and >= 5 { assert (integer % 2 != 0) && (integer >= 5); // a prime is odd and not divisible by every odd integer up to its square root result = true; // assume prime for (int divisor = 3; !done && (divisor * divisor <= integer); divisor = divisor + 2) { if (integer % divisor == 0) { result = false; // divisible; not prime done = true; } // end if } // end for } // end if return result; } // end isPrime // 20.09 class TableEntry<S, T> { private S key; private T value; private boolean inTable; // true if entry is in table private TableEntry(S searchKey, T dataValue) { key = searchKey; value = dataValue; inTable = true; } // end constructor public S getKey() { return key; } // end getKey private T getValue() { return value; } // end getValue private void setValue(T newValue) { value = newValue; } // end setValue private boolean isIn() { return inTable; } // end isIn private boolean isRemoved() // opposite of isIn { return !inTable; } // end isRemoved // state = true means entry in use; false means entry not in use, ie deleted private void setToRemoved() { key = null; value = null; inTable = false; } // end setToRemoved private void setToIn() // not used { inTable = true; } // end setToIn } // end TableEntry } // end HashedDictionary HashedDictionaryTest.java import java.io.*; import java.util.*; public class HashedDictionaryTest { String method; String key; String value; public HashedDictionaryTest(String method, String key, String value){ this.method = method; this.key = key; this.value = value; } public static void main(String[] args) { // declaring nameList as HashedDictionary instead of DictionaryInterface enables display method in HashedDictionary HashedDictionary<Name, String> nameList = new HashedDictionary<Name, String>(11); String line[]= new String[100]; String subline[]=new String[100]; String[] tokens=new String[100]; String subtoken[] =new String[100]; int i=0,j=0,k=0; try{ Scanner scanner = new Scanner(new File("userfile.txt")).useDelimiter(" "); while (scanner.hasNext()) { line[i] = scanner.nextLine(); Scanner scanner1 = new Scanner(line[i]).useDelimiter(" "); while (scanner1.hasNext()) { subline[j] = scanner1.nextLine(); j++; } i++; } String strLine; while ((strLine = subline[k]) != null) { tokens = strLine.split(" "); for(int m=0; m<tokens.length;m++){ subtoken[m]=tokens[m]; } if(tokens.length==1) { subtoken[1]=null; subtoken[2]=null; } else if (tokens.length==2) subtoken[2]=null; HashedDictionaryTest record = new HashedDictionaryTest(subtoken[0],subtoken[1],subtoken[2]);//process record , etc chooseMethod(subtoken[0],subtoken[1],subtoken[2],nameList); k++; } } catch (FileNotFoundException e) { e.printStackTrace(); } } public static void chooseMethod(String s , String s1 , String s2 ,HashedDictionary<Name, String> nameList ) { if (s.equals("add")) nameList.add(new Name(s1),s2); else if (s.equals("print")) nameList.display(); else if(s.equals("locate")) nameList.locate( nameList.getHashIndex(new Name(s1)),new Name(s1)); else if (s.equals("remove")) { int index =nameList.getHashIndex(new Name(s1)); index=nameList.hashTable.length-index; Name m= (Name)nameList.hashTable[index-1].getKey(); nameList.remove(m); } } } // end HashedDictionaryTest Name.java /** This class is like the one in the folder Comparable, * but adds a constructor and hashCode for testing purposes. */ public class Name { private String first; // first name private String last; // last name public Name() { this("",""); } // end default constructor public Name(String firstName) // for testing *************** { this(firstName, ""); } // end constructor public Name(String firstName, String lastName) { first = firstName; last = lastName; } // end constructor @Override public int hashCode() // for testing *************** { // this hash code causes collisions int h = 0; for (int i = 0; i < first.length(); i++) { h = h + first.charAt(i); } return h; // a reasonable hash code follows: // return first.hashCode() + last.hashCode(); } // end hashCode public void setName(String firstName, String lastName) { setFirst(firstName); setLast(lastName); } // end setName public String getName() { return toString(); } // end getName public void setFirst(String firstName) { first = firstName; } // end setFirst public String getFirst() { return first; } // end getFirst public void setLast(String lastName) { last = lastName; } // end setLast public String getLast() { return last; } // end getLast public void giveLastNameTo(Name aName) { aName.setLast(last); } // end giveLastNameTo @Override public String toString() { return first + " " + last; } // end toString @Override public boolean equals(Object other) { boolean result; if ((other == null) || (getClass() != other.getClass())) result = false; else { Name otherName = (Name)other; result = first.equals(otherName.first) && last.equals(otherName.last); } // end if return result; } // end equals } // end Name userFile.txt add 555-1234 Tabatha add 555-1235 Toni print locate Toni remove Tabatha add 555-1236 Tobbie print locate Tabatha
Quadratic Probing And Linear Probing : Java Program Source Code
 Reviewed by Anonymous J
on
06:49:00
Rating:
Reviewed by Anonymous J
on
06:49:00
Rating:
 Reviewed by Anonymous J
on
06:49:00
Rating:
Reviewed by Anonymous J
on
06:49:00
Rating: